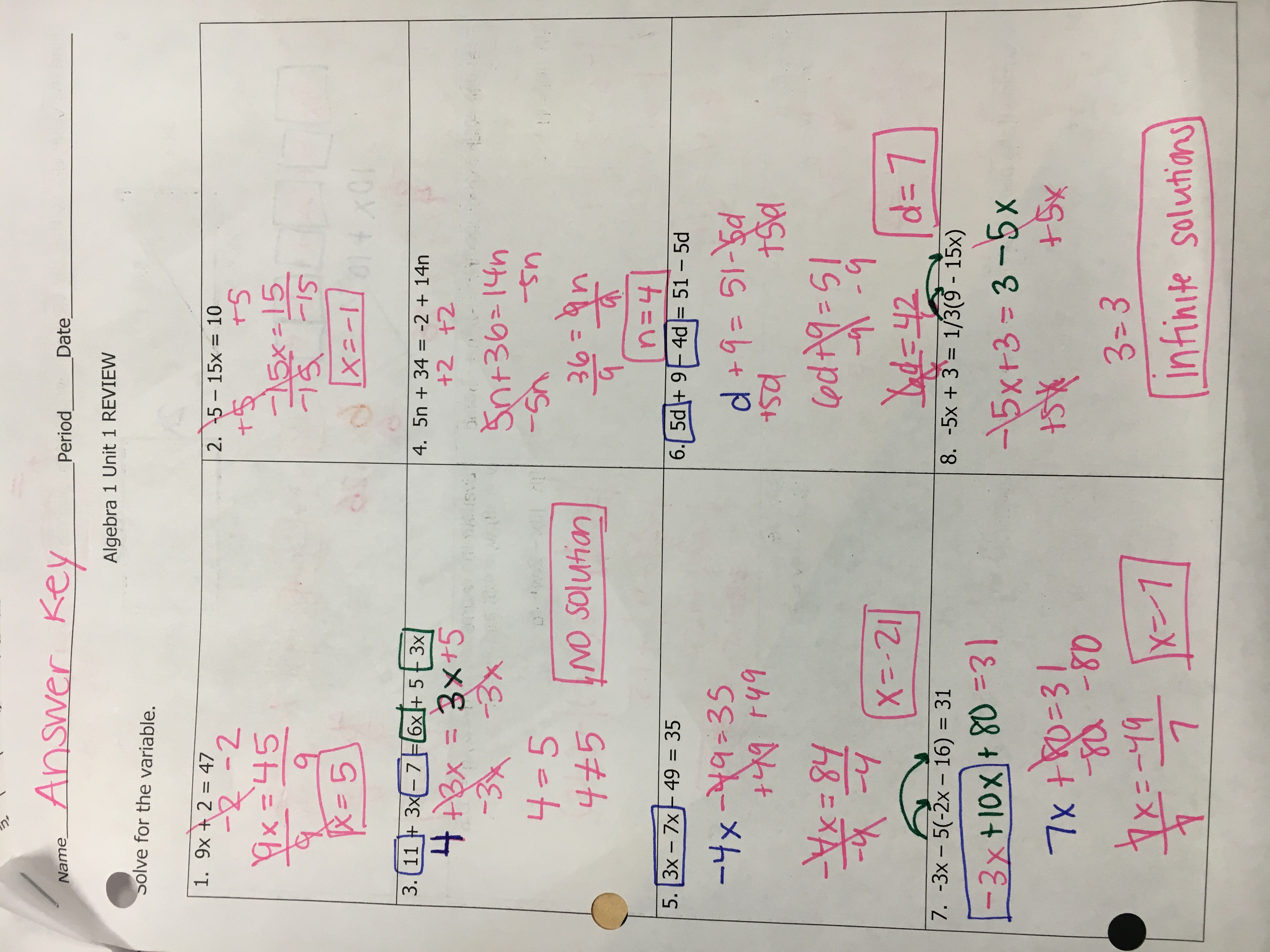
Understanding Unit 1 Homework 2: Expressions And Operations

Adam Koss 17 Jul 2025

Are you looking at your homework and seeing "Unit 1 Homework 2: Expressions and Operations" and feeling a bit unsure? Well, you are certainly not alone. Many students find these early topics a little tricky, and that is perfectly okay. This part of your studies is really important because it builds a strong base for so much of what you will learn next in math or even in computer programming, you know, later on.

This homework, Unit 1 Homework 2 Expressions and Operations, is all about getting comfortable with the basic building blocks of mathematics. It helps you work with numbers and symbols in a structured way. You will learn how to put things together and how to take them apart, in a sense, using rules that everyone agrees on. It is like learning the grammar of math, really.

When we talk about "units," it can mean so many different things. For example, my text, which discusses things like "unit 6 to unit 9 tutorials on learn.unity website" or "NUnit unit test," is talking about units in a very specific, technical way, often in the world of software or game creation. But for you, right now, "Unit 1" probably means something quite different, a starting point in your current course. So, let's get into what your Unit 1 Homework 2 is likely asking you to do.

What Are Expressions?
- Numerical Expressions
- Algebraic Expressions
Understanding Operations
- The Four Basic Operations
- Other Common Operations
The Order of Operations
- Why Order Matters
- Remembering the Order
Evaluating Expressions
- Step-by-Step Evaluation
- Working with Variables
Common Mistakes to Avoid
Practice Makes Perfect
Frequently Asked Questions (FAQs)

What Are Expressions?

So, what exactly is an expression in math? Well, it is a combination of numbers, variables, and operation symbols. It is not a complete sentence like an equation is, because it does not have an equals sign. An expression is more like a phrase or a piece of a mathematical idea. You can think of it that way, you know.

Numerical Expressions

A numerical expression is a math phrase with just numbers and operation symbols. There are no letters involved here. For instance, `3 + 5` is a numerical expression. Another one could be `10 - 2 * 4`. These expressions have a value that you can figure out. You can actually calculate what they are worth. They are very straightforward, in a way.

Let's look at some examples, you know.

`7 + 3`
`12 / 4`
` (5 - 2) * 6 `

Each of these, you see, can be worked out to a single number. They are pretty clear about what they mean.

Algebraic Expressions

Now, an algebraic expression is a bit different. It has numbers, operation symbols, and at least one variable. A variable is usually a letter, like `x` or `y`, that stands for an unknown number. So, `x + 7` is an algebraic expression. Another one might be `2y - 5`. You cannot find a single numerical value for these until you know what the variable stands for. It's like having a placeholder, basically.

Here are some examples of algebraic expressions, you know:

`a - 9`
`4 * b + 1`
` (z + 3) / 2 `

To work these out, you would need to be given a value for `a`, `b`, or `z`. That is how they work, really.

Understanding Operations

Operations are the actions you perform on numbers or variables. They tell you what to do. You have probably been doing these for a long time without even thinking about them as "operations." They are the verbs of math, if you think about it like that.

The Four Basic Operations

There are four basic operations that you will use all the time, you know. These are the building blocks for almost everything else. Getting really good at these is a big help.

1. **Addition (+):** This means combining numbers. When you add, you find the total or sum. For example, `5 + 3` makes `8`. It is like putting things together, in a way.

2. **Subtraction (-):** This means taking one number away from another. When you subtract, you find the difference. For example, `10 - 4` makes `6`. It is about finding what is left, basically.

3. **Multiplication (* or x or .):** This means adding a number to itself a certain number of times. When you multiply, you find the product. For instance, `6 * 2` means `6 + 6`, which makes `12`. It is a quick way to do repeated addition, you know.

4. **Division (/ or ÷):** This means splitting a number into equal groups. When you divide, you find the quotient. For example, `15 / 3` makes `5` because you can make five groups of three from fifteen. It is about sharing or grouping, really.

Other Common Operations

Beyond the basic four, you will also come across other operations, especially as you move forward in your Unit 1 Homework 2. These include things like exponents and parentheses. They are very common, too.

1. **Exponents:** An exponent tells you how many times to multiply a base number by itself. For example, `2^3` means `2 * 2 * 2`, which makes `8`. The small `3` up high is the exponent. It is a shorthand for repeated multiplication, you know.

2. **Parentheses ( ):** These are used to group parts of an expression. They tell you to do the operations inside them first. For example, in `(2 + 3) * 4`, you would add `2` and `3` first to get `5`, then multiply by `4` to get `20`. They are like little instructions to prioritize, basically.

The Order of Operations

This is probably the most important part of Unit 1 Homework 2 Expressions and Operations. If you do not follow the correct order, you will get the wrong answer every time. It is a set of rules that everyone agrees on so that math problems have only one correct answer. It is a bit like following a recipe, you know, steps in a certain sequence.

Why Order Matters

Imagine you have the expression `6 + 4 * 2`. If you add `6 + 4` first, you get `10`, then `10 * 2` makes `20`. But if you multiply `4 * 2` first, you get `8`, then `6 + 8` makes `14`. See how you get two different answers? This is why the order of operations is so important. It makes sure everyone gets the same answer, every single time. It is about consistency, really.

Remembering the Order

There is a popular way to remember the order of operations. It is often taught as PEMDAS or BODMAS. Both mean the same thing, just with slightly different words. Let's look at PEMDAS, as it is very common, too.

1. **P**arentheses: Do everything inside parentheses first. If there are nested parentheses (one set inside another), work from the innermost ones outward. This is the first step, basically.

2. **E**xponents: After parentheses, deal with any exponents. This means figuring out `2^3` or `5^2` and so on. This comes next, you know.

3. **M**ultiplication and **D**ivision: These two operations are done next, from left to right. They have the same priority. So, if you see both multiplication and division, just work them out as they appear from the left side of the expression to the right side. It is like reading a book, in a way.

4. **A**ddition and **S**ubtraction: Finally, do addition and subtraction, also from left to right. They also have the same priority. Just like multiplication and division, you just work them out as they come up from left to right. This is the last step, really.

So, for `6 + 4 * 2`, using PEMDAS:

No Parentheses.
No Exponents.
Multiplication: `4 * 2` makes `8`. The expression becomes `6 + 8`.
Addition: `6 + 8` makes `14`.

The correct answer is `14`. This system helps you get it right, every time, you know.

Evaluating Expressions

When your homework asks you to "evaluate an expression," it means you need to find the single numerical value of that expression. If it is a numerical expression, you just follow the order of operations. If it is an algebraic expression, you will usually be given values for the variables. Then you substitute those values in and calculate. It is a pretty simple process, really.

Step-by-Step Evaluation

Let's try an example: Evaluate `18 / 3 + 5 * (7 - 4)`.

**Parentheses first:** `(7 - 4)` makes `3`. The expression becomes `18 / 3 + 5 * 3`.
**Exponents next:** No exponents here.
**Multiplication and Division (left to right):** * `18 / 3` makes `6`. The expression is now `6 + 5 * 3`. * `5 * 3` makes `15`. The expression is now `6 + 15`.
**Addition and Subtraction (left to right):** * `6 + 15` makes `21`.

So, the value of the expression is `21`. Breaking it down like this helps a lot, you know.

Working with Variables

Now, let's evaluate an algebraic expression. Say you need to evaluate `2x + 3y` when `x = 4` and `y = 2`.

**Substitute the values:** Replace `x` with `4` and `y` with `2`. The expression becomes `2 * 4 + 3 * 2`.
**Multiplication first:** * `2 * 4` makes `8`. * `3 * 2` makes `6`. The expression is now `8 + 6`.
**Addition last:** * `8 + 6` makes `14`.

The value of the expression is `14`. It is like filling in the blanks, in a way. Learn more about expressions and operations on our site, there is quite a bit to cover.

Common Mistakes to Avoid

When working on Unit 1 Homework 2 Expressions and Operations, people sometimes make a few common errors. Being aware of these can help you avoid them, you know. It is good to know what to watch out for.

1. **Not following the order of operations:** This is the biggest one. Always, always, remember PEMDAS. Doing operations out of order is the quickest way to get a wrong answer. It is very important, really.

2. **Careless with negative numbers:** When you have subtraction or negative numbers, be extra careful. For example, `5 - (-3)` is actually `5 + 3`, which makes `8`. A lot of people mix this up. It is a bit tricky, that.

3. **Misinterpreting multiplication:** Remember that a number next to a variable, like `2x`, means `2 * x`. Sometimes people forget that the multiplication symbol is implied. It is just a common shorthand, you know.

4. **Rushing:** Taking your time and doing one step at a time helps prevent errors. It is better to go slow and be right than to rush and be wrong. Patience helps a lot, basically.

Practice Makes Perfect

The best way to get good at Unit 1 Homework 2 Expressions and Operations is to practice. Do as many problems as you can. The more you work through them, the more natural it will feel. You will start to see the patterns and the rules will become second nature. It is really just about repetition, you know.

Do not be afraid to ask for help if you get stuck. Your teacher, a friend, or even online resources can be very useful. There are many places to find extra practice problems or explanations if you need them. You can find more practice problems and explanations on this page here.

Remember, everyone starts somewhere. What seems hard now will become much easier with a little effort and consistent practice. You can totally get this, you know.

Frequently Asked Questions (FAQs)

Here are some questions people often ask about expressions and operations, you know.

What is an expression in math?
An expression in math is a combination of numbers, variables, and operation symbols, but it does not have an equals sign. It is a mathematical phrase that represents a value, like `7 + x` or `(5 * 2) - 3`. It is not a complete equation, basically.

What are the basic operations in math?
The basic operations in math are addition (+), subtraction (-), multiplication (*), and division (/). These are the fundamental actions you perform on numbers to combine them, separate them, or find their totals or parts. They are the core actions, really.

How do you evaluate an algebraic expression?
To evaluate an algebraic expression, you first substitute the given numerical values for each variable. After that, you follow the order of operations (PEMDAS/BODMAS) to calculate the single numerical value of the expression. It is a two-step process, you know.

For more detailed explanations and examples, you might want to check out resources on a trusted educational site, perhaps like this one: Math Resource. It is a good place to get more help, too.

Getting a handle on Unit 1 Homework 2 Expressions and Operations is a big step. It sets you up for so much more. Keep practicing, and you will do great. It is all about building those skills, you know.

Unit Linear Equations Homework 1 Simplifying Expressions Answer Key

Unit 1 Homework[ 3515] - homework questions - Studocu

Simplifying Rational Expressions (A) Worksheet | Algebra II PDF

Celebrity Casting News