Simplifying Unit 11 Volume And Surface Area Homework 5: Your Latest Guide
Are you feeling a bit stuck on Unit 11 Volume and Surface Area Homework 5? It's a common feeling, you know. Figuring out shapes in three dimensions can seem like a big puzzle sometimes. This particular homework set, Unit 11 Volume and Surface Area Homework 5, often brings up questions about how much space something takes up or how much material you need to cover its outside. We are going to look at these ideas together, making them much clearer for you. So, too it's almost like finding the right tutorial when you really need one, just like how people look for answers on forums.
Lots of students find this topic a bit tricky. They might wonder about the right formulas to use. Or, perhaps, they struggle with seeing how a flat shape becomes a solid one. That, is that, a big part of the challenge for many. This guide aims to help you get a solid grasp on the homework, making those concepts click into place. We will go through the steps, giving you practical ways to approach each problem.
Understanding volume and surface area is a really useful skill. It helps in many everyday situations, more or less. Think about packing a box or painting a room. These tasks use the same math you will see in Unit 11 Volume and Surface Area Homework 5. This article gives you a fresh look at these ideas. It offers simple explanations and tips you can use right away. We will make sure you feel much more ready for your tasks.
- Academy Nightclub Los Angeles
- Super Mrkt Los Angeles
- Kyle Paul Hofstetter Obituary
- Watson Supply Weed
- Strip Club After Hours
Table of Contents
- Understanding the Basics of Volume and Surface Area
- Common Shapes in Unit 11 Homework 5
- Key Formulas for Your Homework
- Tackling Unit 11 Volume and Surface Area Homework 5 Problems
- Frequently Asked Questions
- Moving Forward with Volume and Surface Area
Understanding the Basics of Volume and Surface Area
When you start Unit 11 Volume and Surface Area Homework 5, it helps to know what these terms really mean. They sound fancy, but they are pretty simple concepts, in a way. We use them to describe three-dimensional objects. Think about any object you can hold in your hand. It has length, width, and height. Volume and surface area help us measure different aspects of such objects.
Understanding these basic ideas makes the homework much easier. It gives you a good foundation. You can build on that knowledge as you go through more complex problems. So, it is a good idea to get these clear in your mind first.
What is Volume?
Volume tells us how much space an object takes up. Imagine filling a container with water. The amount of water that fits inside is its volume. It is a measure of capacity. We measure volume in cubic units. This means cubic centimeters, cubic meters, or cubic inches, for example. You know, like how some discussions on Sep 13, 2020, were about "SI units" for measurement. That, is that, a similar idea here.
- Triple F Vintage Store
- Fresh And Fancy Farms Photos
- Cloud Smoke Shop Nutley
- 58 Bridge Ave Bay Head Nj
- Mr Pink Energy Drink
Every three-dimensional object has a volume. A box, a ball, a can—they all take up space. Knowing how to find volume is very useful. It helps you figure out how much something holds. This is a very practical skill, you know.
What is Surface Area?
Surface area tells us the total area of all the surfaces of a three-dimensional object. Imagine wrapping a gift. The amount of wrapping paper you need to cover the entire gift is its surface area. It is a measure of the outside covering. We measure surface area in square units. This means square centimeters, square meters, or square inches, for example.
Think about painting a wall. You need to know the wall's surface area to buy enough paint. This concept applies to many things. It is about covering the outside of something. So, it is a different kind of measurement than volume, yet very important.
Common Shapes in Unit 11 Homework 5
Unit 11 Volume and Surface Area Homework 5 often focuses on a few common shapes. You will see prisms, cylinders, pyramids, cones, and spheres. Each shape has its own way of calculating volume and surface area. Getting to know these shapes well helps a lot. It makes the homework less intimidating, apparently.
We will look at each one. We will talk about what makes them special. Knowing their characteristics helps you choose the right formula. It is like knowing the different tools in a toolbox, more or less.
Prisms and Their Properties
A prism is a solid object with two identical ends. These ends are called bases. They are parallel to each other. The sides of a prism are flat surfaces. They are rectangles. Think of a cereal box. That is a rectangular prism. A triangular prism has triangles as its bases.
The name of a prism comes from the shape of its base. So, a rectangular prism has rectangular bases. A triangular prism has triangular bases. This is quite simple, you know. Understanding this helps you identify the parts for your calculations.
Cylinders and Their Properties
A cylinder is a solid object with two circular bases. These bases are parallel. The side of a cylinder is a curved surface. Think of a soup can. That is a cylinder. It is like a prism, but with circular bases instead of polygons.
Cylinders are very common in everyday life. We see them everywhere. Knowing how to work with them is very useful. Their circular nature means you will often use pi (π) in your calculations. This is a key point, you know.
Pyramids and Their Properties
A pyramid is a solid object with a polygon as its base. Its sides are triangles. These triangles meet at a single point at the top. This point is called the apex. The most famous pyramids have square bases, like those in Egypt. But, a pyramid can have any polygon as its base, actually.
The height of a pyramid is important. So is its slant height. The slant height is the height of one of the triangular faces. You will need to know the difference for your homework. This is a bit tricky, but practice helps, you know.
Cones and Their Properties
A cone is a solid object with a circular base. It has a curved surface that tapers to a single point. This point is the apex. Think of an ice cream cone. That is a cone. It is like a pyramid, but with a circular base.
Just like pyramids, cones have a height and a slant height. You will use pi (π) when working with cones, too. Understanding how these parts relate helps with the formulas. It is pretty similar to cylinders in that way.
Spheres and Their Properties
A sphere is a perfectly round three-dimensional object. Every point on its surface is the same distance from its center. Think of a basketball or a globe. That is a sphere. It has no flat surfaces or edges, you know.
The main measurement for a sphere is its radius. The radius is the distance from the center to any point on the surface. Spheres are unique because their volume and surface area formulas are quite different from other shapes. They do not have bases or height in the usual sense, basically.
Key Formulas for Your Homework
The heart of Unit 11 Volume and Surface Area Homework 5 is using the right formulas. Each shape has its own specific formulas for volume and surface area. Knowing these by heart helps a lot. It makes solving problems much faster, you know.
We will list the most common ones you will need. Make sure you understand what each part of the formula means. This is more important than just memorizing them. It helps you apply them correctly, too it's almost like knowing why a certain code works in programming.
Volume Formulas
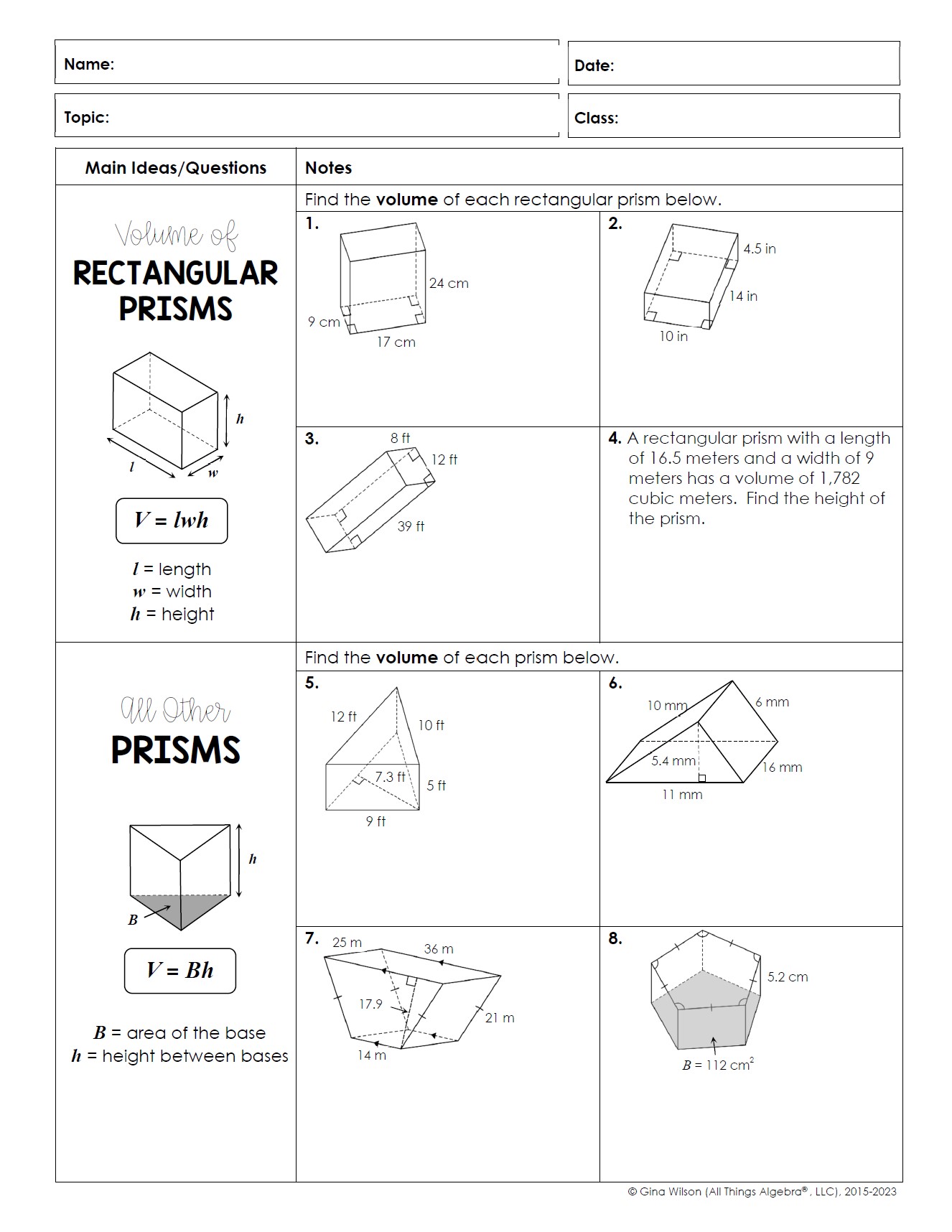
Rectangular Prism: Volume = length × width × height (V = lwh)
This is a very basic one. You just multiply the three dimensions. It is pretty straightforward, you know.
Cylinder: Volume = π × radius² × height (V = πr²h)
Remember that 'r' is the radius of the circular base. The 'h' is the height of the cylinder. Pi (π) is about 3.14159, or you might use the pi button on your calculator. This formula is pretty common.
Pyramid: Volume = (1/3) × base area × height (V = (1/3)Bh)
Here, 'B' stands for the area of the base. If the base is a square, you find its area first. Then you multiply by the height and by one-third. This is a bit different, you know.
Cone: Volume = (1/3) × π × radius² × height (V = (1/3)πr²h)
This is very similar to the cylinder formula, but you multiply by one-third. It is a common pattern for shapes that come to a point. This is quite useful to remember.
Sphere: Volume = (4/3) × π × radius³ (V = (4/3)πr³)
This formula only needs the radius. The 'r³' means radius multiplied by itself three times. This one is unique to spheres, you know.
Surface Area Formulas
Rectangular Prism: Surface Area = 2(lw + lh + wh)
This formula adds up the area of all six faces. You have two of each pair of sides. It is like finding the area of three different rectangles and then doubling that sum. This is pretty much covering all sides.
Cylinder: Surface Area = 2πr² + 2πrh
The '2πr²' part is for the two circular bases. The '2πrh' part is for the curved side. Imagine unrolling the side of a can; it would be a rectangle. This formula covers all parts, basically.
Pyramid: Surface Area = Base Area + (1/2) × perimeter of base × slant height (SA = B + (1/2)Pl)
Here, 'B' is the area of the base. 'P' is the perimeter of the base. 'l' is the slant height. You need to be careful to use the slant height, not the regular height. This is a common point of confusion, you know.
Cone: Surface Area = πr² + πrl
The 'πr²' part is for the circular base. The 'πrl' part is for the curved side. Again, 'l' is the slant height. This is similar to the pyramid, but with circles instead of polygons. It is quite logical, you know.
Sphere: Surface Area = 4πr²
This formula only needs the radius. It is a simple one, in some respects, for a sphere. It is very different from other shapes. This is just how it works for round objects.
Tackling Unit 11 Volume and Surface Area Homework 5 Problems
Now that you know the shapes and formulas, let's talk about how to approach the problems in Unit 11 Volume and Surface Area Homework 5. It is not just about plugging numbers into a formula. There is a way to think about each problem. This makes it easier to get the right answer, you know.
A good strategy helps you break down complex problems. It makes them manageable. We will look at a step-by-step method. We will also talk about common mistakes. Avoiding these mistakes saves you time and frustration, you know.
Step-by-Step Problem Solving
Read the problem carefully: Understand what the question is asking. Are you looking for volume or surface area? What shape is involved? This is the very first step, you know.
Sometimes problems give extra information you do not need. Or, they might give you something you need to convert, like diameter instead of radius. Be aware of these details.
Identify the shape: Is it a prism, cylinder, pyramid, cone, or sphere? This helps you pick the right formula. It is like identifying the "unit" of study, just as people might ask about "unit 6 to unit 9 tutorials" when learning something new.
Drawing a picture of the shape can help too. Label the dimensions you are given. This visual aid makes things much clearer, actually.
Write down the formula: Once you know the shape and what you need to find, write down the correct formula. This helps you organize your thoughts. It also reminds you what information you need.
Having the formulas handy, perhaps on a formula sheet, is very useful. You do not want to guess here, you know.
List the given values: Write down all the measurements you are given. Make sure you use the correct units. If you are given a diameter, remember to find the radius. This is a common point to check.
Double-check your numbers before you start calculating. A small error here can mess up the whole problem, you know.
Substitute values into the formula: Put the numbers you have into the formula. Be careful with calculations. Use a calculator if you need to. This is where precision matters, you know.
Show your work. This helps you track your steps. It also makes it easier to find mistakes if you make any. This is good practice, you know.
Calculate the answer: Perform the math operations. Follow the order of operations. Get your final numerical answer. This is the goal, after all.
Take your time with this step. Rushing can lead to simple errors. It is better to be slow and accurate.
Include the correct units: Volume answers need cubic units (e.g., cm³). Surface area answers need square units (e.g., cm²). This is very important. It shows you understand the meaning of your answer. Just like understanding "newton meter SI units" in physics, knowing the right unit for your answer in math is key.
Always write down the units. It is a small detail, but it is a very important one. Your answer is not complete without them, you know.
Tips for Avoiding Common Mistakes
Mixing up volume and surface area: These are different concepts. Make sure you know which one the problem asks for. Sometimes students use a volume formula when they need surface area, or vice versa. This is a common mix-up, you know.
Read the question again if you are unsure. The wording often gives a clue. For example, "how much can it hold" points to volume. "How much material to cover" points to surface area.
Using diameter instead of radius: Many formulas use the radius (r). If the problem gives you the diameter (d), remember that the radius is half of the diameter (r = d/2). This is a very frequent error, you know.
Always check if you have the radius or diameter. It is a quick check that saves a lot of trouble. This is a critical step, you know.
Incorrectly calculating base
- Ts Jenny Wonders
- Autumn Nelson Big Ass
- Airbnb Interior Design Services
- Cole Young Metalwood
- Watson Supply Weed
Solved: Unit 11: Volume & Surface Area Homework 1: Area of Plane

Unit 11 Surface Area and Volume - North Junior High 8th Grade Math
Geometry Unit 11: Volume & Surface Area - All Things Algebra®